One of the phenomenons of probability is Gambler’s Ruin. The most common meaning is that a gambler with finite wealth, playing a fair game (that is, each bet has expected zero value to both sides) will eventually go broke against an opponent with infinite wealth.
In other words, the maxim of gambler’s ruin is that if you play long enough you will eventually go bankrupt and have to quit the game prematurely.
 Collage of Shutterstock images; Foreground: wacpan, Background: Lisa S.
Collage of Shutterstock images; Foreground: wacpan, Background: Lisa S.The World of Sports Betting
The truth is that in the world of sports betting, the common gambler has far less money than a bookmaker or casino, and there will inevitably be a time when he will simply be unable to continue playing and, of course, the house will not be giving credit.
“Long enough” may be a very long time though. It mainly depends on how much money the gambler starts with, how much he bets, and the odds of the game. Even with better than even odds, the gambler will eventually go bankrupt. But, this may take a very long time indeed.
Please note that we are talking here about a “fair” game; e.g. each bet with zero value. The practice of bookmakers and betting sites to offer odds with an overround in their favour makes this outcome just much quicker.
Fair Coin Flipping
To make the dilemma of gambler’s ruin a little easier to understand imagine coin flipping with a friend. You each have a finite number of pennies (n1 for yourself and n2 for your friend).
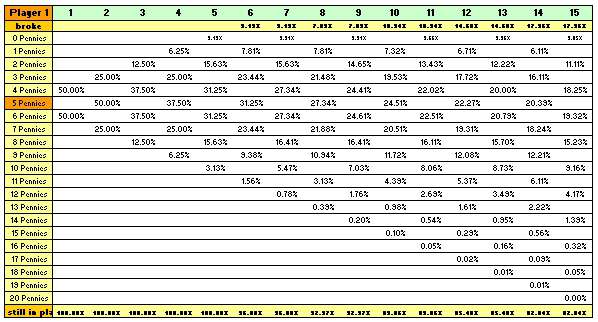
Now, flip one of the pennies (either player). Each player has a 50% probability of winning (head or tail). If it’s a head you win a penny and if it’s a tail you surrender a penny to your friend. Repeat the process until one of you has all the pennies.
If this process is repeated indefinitely, the probability that one of you will eventually lose all his pennies is 100%. In fact, the chances P1 and P2 that players one and two, respectively, will be rendered penniless are:

Now let’s populate these equations with real numbers:
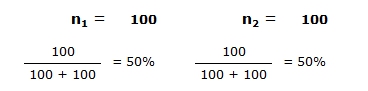
The above example is based on both players starting with the same amount of pennies (100 each). In other words, you and your friend have both an exact probability of 50% to end up with all of the pennies after many, many coin flips. This means that after an unknown number of coin flips either you or your friend will finish banking all the pennies. At the start, your chances are equal, and it is impossible to say who may win.
However, if one of you has many more pennies than the other, say you start with 100, and your friend with 10,000, then your chance of finishing with all of the pennies (yours as well as your friend’s) is as low as 1%, whilst your friend’s chances are 99% to win this unequal match.
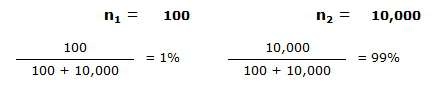
Bankruptcy Probability Table – Gambler’s Ruin
To visualize the gambler’s ruin problem further, here is an overview of the probabilities of finishing with N amount of pennies.
Player 1 starts with 5 pennies. Player 2 has an infinite amount of pennies.
The top row shows the number of flips. The left hand column shows player 1’s current amount of money. The numbers in the table are probabilities (click on the image to enlarge; opens in a new tab):
Reading the table (examples):
After the first flip player 1 has a 50/50 chance of ending up either with 4 pennies (i.e. he lost the first coin flip), or with 6 pennies (i.e. he won the first coin flip).
In 10.4% of the trials player 1 will be broke (penniless) after the tenth flip of the coin. This means that every 10th experiment of this nature player 1 will have been forced to give up after the 10th flip of the coin due to a run of “bad luck” whilst player 2 is not affected by “bad luck” purely because he has plenty of coins to sit through and survive any such spell.
82.04% of the players will still be in the game after coin flip 15. However, 17.96% of the gamblers will already have retired due to exhausted funds.
In return for this freebie we would appreciate if you could share this article or give us a ‘thumbs-up’ with a ‘love’ or ‘like’ via Twitter or Facebook or any other social network site 🙂
Of course, you will now probably surmise that player 1 started with only 5 pennies, and by staking 1 penny each bet he was risking 20% of his starting bank on each coin flip, which is way too much. Player 1 should ideally have started with a much larger pile of pennies, and risked a far smaller percentage of his bank with each coin flip.
Anyway, eventually the same thing will always happen, albeit just much more slowly. Player 1 will still go broke sooner or later, if player 2 has an infinite amount of pennies. It’s just for the sake of the above table and illustration that we choose to show the calculations with a starting bank of 5 pennies only.
Continue reading, to see some more examples and illustrations…
Visualisation and Demonstration of the Gambler’s Ruin
If you start with only 5 pennies, and your opponent with 10,000 pennies, then your chances are as little as 0.04975% to survive (not to go bankrupt), and furthermore you may have to play as many as 50,000 games to beat your opponent!
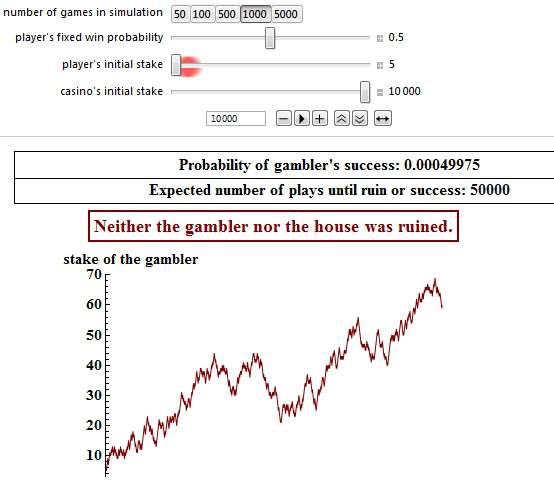
However, in the majority of cases (99.95%) player 1 will pretty soon be bankrupt, like in this simulation:
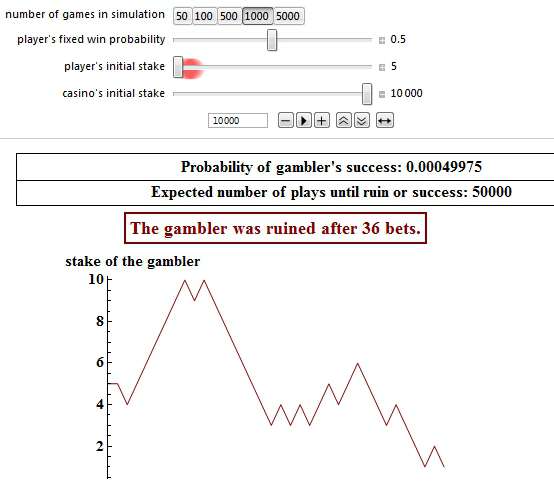
Please note that both snapshots above have had the same starting point. Player 1’s initial stake was 5 pennies and his opponent’s initial bank was 10,000. It is just that the events developed in different directions, hence a completely different outcome.
Starting with a Higher Starting Bank
If you start with a somewhat higher starting bank than just 5 pennies, say, 50 pennies, and then risk only 1% of your bank (1 penny each bet), your chances of survival increase from 0.04975% (starting with 5 pennies) to 0.497512% (of not going broke). However, this time you may have to wait 500,000 betting rounds to conquer your opponent!:
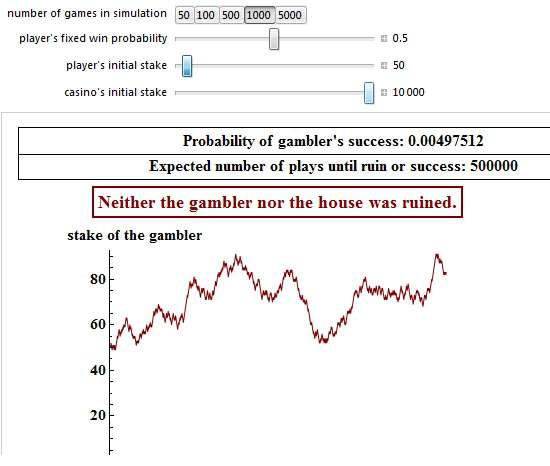
Although the above simulation shows some success after 1,000 bets, you must not forget, that in 99.5% of all attempts, even a starting bank of 50 pennies will still lead to bankruptcy, like in the following simulation. It took a little bit longer than the 36 coin flips on the previous page, but nevertheless the gambler was ruined after 631 bets:
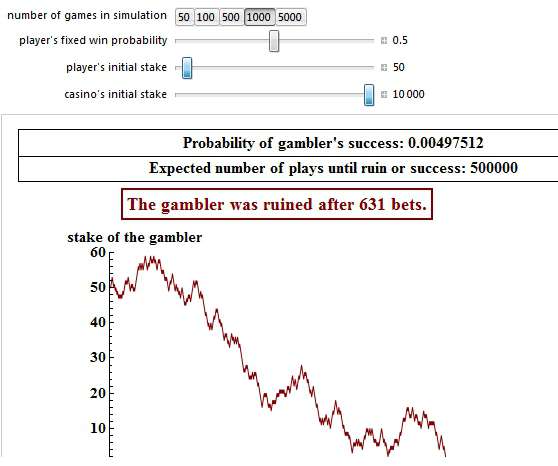
Starting with a Larger Starting Bank
Aware of the gambler’s ruin dilemma, the gambler now increases his bank to 500 pennies and only risks 0.2% of his betting bank per bet. His chances to beat the bookie increase to 4.76%, but only if the bookie did not start with more than 10,000 pennies himself. In 95.24% of the cases, despite the higher starting bank the gambler will lose still everything and the house will win.
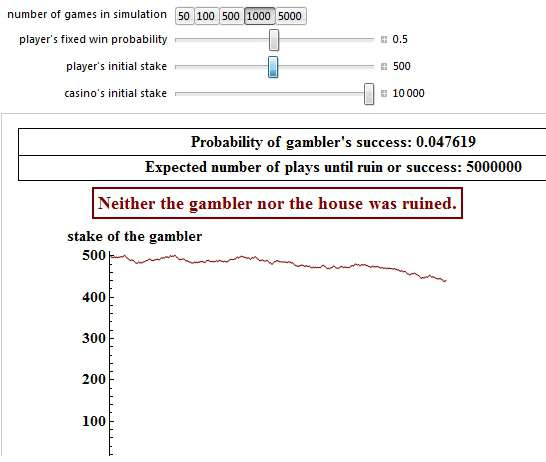
To put a long story sideways, the gambler’s ruin dilemma essentially dictates that a gambler with finite wealth, playing a fair game will eventually go broke against an opponent with infinite wealth. The player starting out with the smallest number of pennies has the greatest chance of going bankrupt. The less pennies player 1 starts with, the greater his chances of bankruptcy.
There is no question that bookmakers have much higher funds than individual punters. This simple principle therefore provides bookmakers with a huge advantage in the long run. As bookmakers offer odds with an overround in their favour the threat of bankruptcy just looms much quicker for the gambler.
Summary
This article explained the Gambler’s Ruin conundrum when betting at zero odds. Of course, the probabilities of winning favour the gambler if he achieves a long-term mathematical advantage and bets on VALUE.
ONLY BY BETTING WITH VALUE ON YOUR SIDE CAN YOU EVER HOPE TO BEAT THE BOOKMAKER OR THE HOUSE.
Check out our odds calculation course, which teaches you how to identify “value” and how to compete with the bookmakers on level terms.
You may also find our sophisticated Excel spreadsheets useful in identifying value bets
Acknowledgements:
The snapshots on pages 3 to 5 of this article (simulations/visualizations) are taken from the WolframMathsWorld demonstrations project.
Our sincere thanks to the WolframAlpha team for providing the public with such useful mathematical information and simulations – Hopefully we have been able to interpret them in layman’s language for you!